Mars Horizon

As you may know - becouse planets and moons aren't flat but more like a sphere, we have horizons.
Horizon is the maximal distance at which we could see other objects.
It is the distance at which we see that the sky connects with earth.
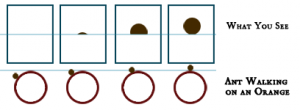
The thing is about computer games, that they completely forgot about horizon and make simple-flat maps.
This isn't a problem when it comes to small areas, but in MCO where you will have large distances with no objects in the way you will see the flat-earth paradox...and it will propably look VERY unreal to the players.
The problem is even worse on Mars, becouse since the planet is smaller, the horizon is also closer.
A regular person standing an a flat Mars-ground would notice that the horizon is closer than on the Earth.
If you walked on moon or mars you would notice an interesting thing - you would reely feel that the earth (in our case: mars) would be somehow cut-down in the middle, but no matter how far you would go ahead you would never see where exactly has it been spliced.
The problem of "flat-earth paradox" will be extremely more noticable when you get higher - like on the mountan.
How to calculate the distance to the horizon on any planet.
1. Look up the planet's radius.
2. Know your height above the surface of the planet.
3. Use this formula to solve for distance:
distance = sqrt [ 2 x radius of planet x height above surface + height about surface ^2]
EXAMPLE:
The height of the Mars rover is 4.9 feet which is 1.49352 meters.
The height of Olympus Mons is 16 miles = 25,749.504 meters.
The radius of Mars in meters is 3390000.
= SQRT(h² + 2*h*r)
= SQRT ( 1.49352 m² + 2*1.49352 m* 3390000 m)
= SQRT ( 1.49352 m² + 10,126,065.6 m²)
= SQRT ( 10,126,067.1 m² )
= 3 182.14819 m
~= 1.977 miles.
A few more feet in height wouldn't change this much. A 6 foot person would be able to see about 2 miles to the horizon on Mars. Using this formula we can also determine that you could see a 16 mile high mountain on Mars from 259.63 miles away by using the mountain height as the height.
What is the "flat-earth paradox"?
Imagine that the Earth is flat - in that scenario we will see distance object no matter how far away they are if there are no obstacles in the way. Goying higher woundn't change anything - you would see the same, and the horizon would look several times bigger. The horizon would apear to be much higher above the ground - so higher that you would think that you are inside a big hole.


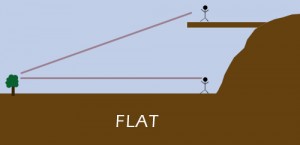
Standing in a flat plateau, you look ahead of you towards the horizon. You strain your eyes, then take out your favorite binoculars and stare through them, as far as your eyes (with the help of the binocular lenses) can see.
Then, you climb up the closest tree – the higher the better, just be careful not to drop those binoculars and break their lenses. You then look again, strain your eyes, stare through the binoculars out to the horizon.
The higher up you are the farther you will see. Usually, we tend to relate this to Earthly obstacles, like the fact we have houses or other trees obstructing our vision on the ground, and climbing upwards we have a clear view, but that’s not the true reason. Even if you would have a completely clear plateau with no obstacles between you and the horizon, you would see much farther from greater height than you would on the ground.
This phenomena is caused by the curvature of the Earth as well, and would not happen if the Earth was flat:

How can it be repaired in MCO?
I see two main options:
a) Make a graphical ilusion near the horizon that will make this happen.
or better
b) Reely make the maps round instead of flat.